To calculate the Natural frequency of vibration for a rectangular cantilever beam with a mass at the free end.
Reference
Hand calculation using known formulas.
Problem
Find the natural frequency of vibration, ω, of the cantilever beam.
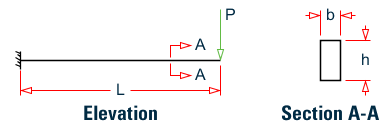
Cantilever beam with mass at free end
Hand Calculations
Stiffness at free end:
k = 3EI/L3 = 45 k/in
Mass
m = w/g = 10.0 k / (386.4 k-sec2/in) = 0.02588 k-sec2/in
Circular frequency:
= 6.637 cycles/sec
Comparison
Table 1. Comparison of results
| Result Type |
Theory |
STAAD.Pro
|
Difference |
| Frequency, f (Hz) |
6.637 |
6.633 |
none |
STAAD Output
CALCULATED FREQUENCIES FOR LOAD CASE 1
MODE FREQUENCY(CYCLES/SEC) PERIOD(SEC)
1 6.633 0.15076
MODAL WEIGHT (MODAL MASS TIMES g) IN KIP GENERALIZED
MODE X Y Z WEIGHT
1 0.000000E+00 1.000514E+01 0.000000E+00 1.000299E+01
MASS PARTICIPATION FACTORS
MASS PARTICIPATION FACTORS IN PERCENT
--------------------------------------
MODE X Y Z SUMM-X SUMM-Y SUMM-Z
1 0.00 99.98 0.00 0.000 99.976 0.000

