Allowable Slenderness Ratio
The allowable slenderness ratio of a member is the limit of the ratio between the effective length and the radius of rotation. The actual slenderness ratio of a member must be less than or equal to the allowable slenderness ratio.
7.2.2 the slenderness ratio of solid web member shall be determined by the following formula according to its instability mode:
- For members whose section
centroid coincides with shear center:
- When calculating the
bending buckling, the slenderness ratio is calculated as follows:
(7.2.2-1) where(7.2.2-1) - and
= - the effective lengths of members to the section principal axis X and Y respectively, in accordance with section 7.4 of this specification;
- and
= - the radius of rotation of the member section to the principal axis X and Y respectively.
- When calculating
torsional buckling, the slenderness ratio shall be calculated according to the
following formula. If the width thickness ratio of biaxially symmetric
cross-section plate does not exceed 15εk, torsional buckling may not be calculated.
where
(7.2.2-3) - , , and
= - polar moment of inertia (MM4), free torsion constant (MM4) and sectorial moment of inertia (MM6) of the shear center of the member's gross section, respectively. For the cross section, can be approximately taken;
= - the effective length of torsional buckling, if both ends are hinged and the end section can be warped freely, the geometric length l is taken; if both ends are clamped and the warpage of end section is completely constrained, it is taken as 0.5l.
- When calculating the
bending buckling, the slenderness ratio is calculated as follows:
- Members with uniaxial
symmetry section:
- The slenderness ratio
should be determined by formula (7.2.2-1) and formula (7.2.2-2) when
calculating the bending buckling around the asymmetric principal axis. The
slenderness ratio should be determined according to the following formula when
calculating the bending torsional buckling around the symmetric principal axis:
where
(7.2.2-4) = - the distance from the centroid of the section to the shear center;
= - the polar radius of rotation of the cross-section of the shear center, for uniaxially symmetric section,
= - the equivalent slenderness ratio of torsional buckling is determined by formula (7.2.2-3).
- When the effective length of the equal leg single angle steel axial compression member is equal, the bending torsion buckling can be omitted. The single angle strut of tower shall comply with the relevant provisions in section 7.6 of this specification.
- The equivalent
slenderness ratio of
T-section members with double angle steel combination around the axis of
symmetry can be determined by the following simplified formula:
where
- b
= - the leg width of equal angle;
- b1
= - the long leg width of unequal angle;
- b2
= - the short leg width of unequal angle;
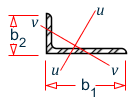
Unequal double angle steel with parallel long legs [Fig. 7.2.2-1 (b)]:
Unequal double angle steel with parallel short legs [Fig. 7.2.2-1 (c)]:
- The members without symmetrical axis and the shear center and centroid do not coincide are not considered in the current program, and are treated as (7.2.2-1) and (7.2.2-2)
- The conversion slenderness ratio of axially compressed members with unequal angle steel can be determined according to the following simplified formula (Fig. 7.2.2-2)
- The slenderness ratio
should be determined by formula (7.2.2-1) and formula (7.2.2-2) when
calculating the bending buckling around the asymmetric principal axis. The
slenderness ratio should be determined according to the following formula when
calculating the bending torsional buckling around the symmetric principal axis:
The allowable slenderness ratio is the allowable slenderness ratio of compression member and tension member. You should select the correct value according to the provisions in 7.4.6 and 7.4.7 of the specification. The default values of the program are: allowable slenderness ratio of 150 under compression and 300 under tension. The slenderness ratio of components mainly includes the following situations:
- Non-seismic:
- The slenderness ratio
of compression members should not exceed the allowable values given in Table
7.4.6
Table 1. Allowable values of slenderness ratio for compression members (Table 7.4.6) Nomenclature of members Allowable values Columns, members of trusses and monitors. 150 Lacing of columns, column bracings beneath crane girders or crane trusses 150 Bracings 200 Members used to reduce the slenderness ratio of compression members 200 Notes:- A slenderness ratio of 200 may be allowed for compression web members in trusses (including space trusses) when they are stressed to or under 50% of their capacities.
- For single angle compression members, the least radius of gyration shall be used for calculation of slenderness ratio, but the radius of gyration about the axis parallel to the leg may be used for calculation of the out-of-plane slenderness ratio in the case of cross diagonals interconnected at the crossing point.
- For trusses with span length equal to or larger than 60m, the allowable slenderness ratio should be taken as 100 for compression chords and end posts, and 150 (when subjected to static or indirect dynamic load), or 120 (when subjected to direct dynamic load) for other web members in compression.
- In case member section is governed by allowable slenderness ratio, the effect of twisting may be neglected in calculating the slenderness ratio.
- The slenderness ratio of
tension members should not exceed the allowable values given in table 7.4.7.
Table 2. Allowable values of slenderness ratio for tension members (Table 7.4.7) Nomenclature of members Structures subject to static or indirect dynamic loading Structures subject to direct dynamic loading Common buildings chord that provides out of plane support for web Mill buildings with heavy duty crane Members of Trusses 350 250 250 250 Column bracings beneath crane girders or crane trusses 300 - 200 - Other tension members, bracings and ties (except pretensioned round bars) 400 - 350 - Notes:- For structures subject to static loading, slenderness ratio of tension members may be checked only in vertical planes.
- For structures subject to direct or indirect dynamic loading, the slenderness ratio of a single angle tension member is calculated similarly to Note 2 of Table 7.4.6.
- The slenderness ratio of bottom chord of crane trusses for medium and heavy duty cranes should not exceed 200.
- In mill buildings equipped with soaking pit cranes and stripper cranes or rigid claw cranes, the slenderness ratio of the bracings (except Item No.2 in the Table) should not exceed 300.
- When tension members change into compression ones under the combined action of dead and wind loads, their slenderness ratio should not exceed 250.
- For trusses with span length equal to or larger than 60m, the slenderness ratio of tension chords and tension web members should not exceed 300 (when subjected to static or indirect dynamic loading) or 250 (when subjected to direct dynamic loading).
- The slenderness ratio
of compression members should not exceed the allowable values given in Table
7.4.6
- Seismic code clause 8.3, 8.4:
Section 8.3.1 states that the slenderness ratio of frame columns shall not be greater than for first grade seismic, shall not be greater than for second grade seismic, shall not be greater than for third grade seismic, and shall not be greater than for fourth grade seismic.
Section 8.4.1 The slenderness ratio and the width-to-thickness ratio of the epicenter diagonal brace shall comply with following requirements:
The slenderness ratio of the epicenter diagonal brace which is designed as compress member shall not be greater than , and the epicenter diagonal brace of the first, second and third seismic grade shall not be designed as tension member, and the slenderness ratio of the epicenter diagonal brace which is designed as tension member shall not be greater than 80 for fourth seismic grade.
- Seismic code clause 9.2.13:
The slenderness ratio of the frame column of the single-story steel factory, which should not be greater than 150 when the axial compression ratio is less than 0.2, and it should not be greater than when the axial compression ratio is not less than 0.2.
The limit of slenderness ratio of the supporting members between columns should meet the requirements of the steel code GB 50017-2017.
- Seismic code clause H.2.8, for
multistory factory structures
H.2.8 the basic anti-seismic structural measures of multi-story steel structure workshop should also meet the following requirements:
- The slenderness ratio of frame column should not be greater than 150; when the axial compression ratio is greater than 0.2, it should not be greater than .
- The width thickness ratio of the frame columns and beams of the workshop shall meet the following requirements:
- In the maximum stress area of frame beam and column, the flange section shall not be changed suddenly, and the upper and lower flange shall be provided with lateral support. The relationship between the support point and the adjacent support point shall meet the relevant requirements of plastic design in steel structure code GB 50017-2017.
- The supporting members between columns should meet the following requirements:
When the program is selected to automatically calculate the slenderness ratio limit, the program will calculate according to the rules in the dialog box. You can select all of them to meet the requirements, or you can specify the filtering calculation rules.