D5.D.6.3 Clause 6.3.2.2 –Elastic critical moment and imperfection factors for LTB checks
The French NA recommends the use of Table 6.3 and 6.4 of NF EN 1993-1-1:2005 to calculate the imperfection factors for Lateral Torsional Buckling (LTB) checks.
The calculation of the LTB reduction factor χLT, requires the calculation of the Elastic Critical Buckling Moment, Mcr. The French NA gives a method to evaluate Mcr in its Annex MCR. This implementation will make use of this method to evaluate Mcr. Annex MCR however deals with the calculation of Mcr for doubly symmetric sections. Hence this implementation will use this method only for doubly symmetric sections. For mono symmetric sections that are symmetric about the minor axis (i.e Tee sections) this implementation will use the method from the NCCI document SN030a-EN-EU as given in the section below. For any other type of section that is not dealt with by the Annex, this implementation will use the method and tables given in Annex F of DD ENV 1993-1-1:1992.
Annex MCR
This document provides a method to calculate Mcr specifically for doubly symmetric sections only. Hence only doubly symmetric sections will be considered for this method in this implementation.
The equation to evaluate Mcr is given as:
C1 and C2 are factors that depend on the end conditions and the loading conditions. The NCCI provides values for C1 and C2 for the different cases as given in Table1 and Table 2 of the Annex. Table 1 deals with the condition of a simply supported member with end moments and the value of C1 is determined by the end moment ratio (Refer to the NA for details). Clause 3.2 of the National Annex however gives a formula to evaluate C1 as:
This formula however does not match the values given in Table 1 of the NA. Hence this implementation will use the values of C1 from Table 1 if the end moment ration (ψ) is exactly equal to the values of ψ in the table. For all other cases this implementation will calculate the value of C1 from equation (6) in the Annex.
The value of C2 will be determined from Table 2 of the Annex based on the loading and end conditions (i.e the CMM parameter in STAAD).
The user will also have the option to specify specific values for C1 and C2 using the C1 and C2 parameters in the design input mode. Refer to D5.C.6 Design Parameters
The French NA considers three separate loading conditions:
- Members with end moments
- Members with transverse loading
- Members with end moments and transverse loading.
The first two cases and its variants can be defined using with the existing CMM parameter values in STAAD.Pro. However the third condition cannot be currently specified in the design input. Hence this implementation will introduce two new values for CMM viz.
CMM 7:Member with varying end moments and uniform loading.
CMM 8: Member with varying end moments and central point load.
The load to moment ratio (μ) will then be used in the calculations will then be used to calculate C1 and C2 as given in section 3.5 of Annex MCR (See Annex MCR in the NA for details).
This implementation will also introduce a new parameter "MU" to be specified when using CMM = 7 or 8. The load to moment ratio (μ) to be used in the calculations is to be input using the new ‘MU’ parameter. This implementation will require that for the French National Annex if CMM = 7 or 8 has been specified, the user should also either specify a value for ‘MU’ or input the values for C1 and C2 using the ‘C1’ and/or ‘C2’ parameters directly.
SN030a-EN-EU – Mono-symmetrical uniform members under bending and axial compression:
This document provides a method to evaluate the elastic critical moment (Mcr) for uniform mono symmetric sections that are symmetric about the weak axis. Hence for this implementation the elastic critical moment for "Tee-Sections" will be worked out using the method in this NCCI.
The equation to evaluate Mcr for mono symmetric sections is given as:
The factors C1, C2, and C3are dependent on the end conditions and loading criteria. This implementation will consider C1, C2, and C3as given in the tables below:
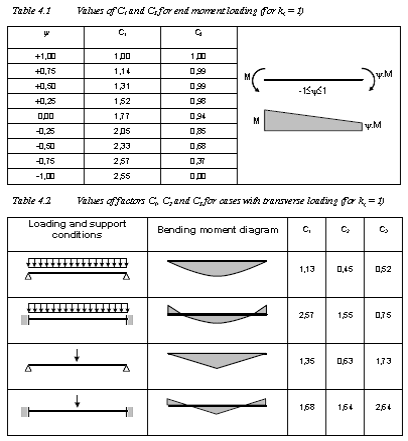
The CMM parameter specified during design input will determine the values of C1, C2 and C3. The default value of CMM is 0, which considers the member as a pin ended member with UDL along its span. This NCCI does not however consider the end moments and transverse loading condition. The user however can use the new "C1", ‘C2’ and ‘C3’ parameters to input the required values for C1, C2 and C3 to be used in calculating Mcr.
Also, the NCCI document and Annex MCR of the FR-NA assume that the member under consideration is free to rotate on plan and that there are no warping restraints for the member( k = kw=1 .i.e., CMN parameter =1.0). Hence the above methods will be used only for members which are free to rotate on plan and which have no warping restraints. For members with partial or end fixities (ie, CMN = 0.5 or CMN = 0.7), this implementation will fall back on to the method and coefficients in DD ENV 1993-1-1:1992.
For all cases that are not dealt with by the National Annex (or the NCCI documents) this implementation will use the method as per the DD ENV 1993-1-1:1992 code.
The term "zg" in the equation to calculate Mcr refers to the distance between the point of application of load on the cross section in relation to the shear center of the cross section. The value of ‘zg’ is considered positive, if the load acts towards the shear center and is negative if it acts away from the shear center. By default, the program will assume that the load acts towards the shear center at a distance equal to (Depth of section/2) from the shear center. The use will be allowed to modify this value by using the ZG parameter. Specifying a value of ZG = 0 in the design input would indicate that the load acts exactly at the shear center of the section so that the term "zg" in the equation will have a value of zero.
