V. Bent Cantilever Deflection
Find deflection due to load at the free end of a cantilever plane bent.
Reference
Kinney, J. S., Indeterminate Structural Analysis, Addison - Wesley Publishing Co., 1957, Page 13, Problem 4 - 38.
Problem
Find the vertical, horizontal and rotational deflection components of point A.
| E = 30,000 ksi |
| I = 200 in4 |
| A = 10 in2 |
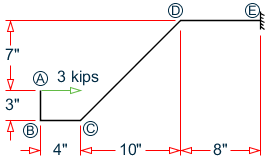
Bent plate frame
Comparison
| Result Type | Theory | STAAD.Pro | Difference |
|---|---|---|---|
| Deflection right, δx (in) | 0.53 | 0.53056 | none |
| Deflection down, δy (in) | 1.16 | -1.17109 | <1% |
| Rotation, θ (rad) | 0.0049 | 0.00488 | none |
STAAD Input
The file C:\Users\Public\Public Documents\STAAD.Pro CONNECT Edition\Samples\ Verification Models\01 Beams\Bent Cantilever Deflection.STD is typically installed with the program.
STAAD PLANE :A CANTILEVER PLANE BENT
START JOB INFORMATION
ENGINEER DATE 18-Sep-18
END JOB INFORMATION
*
* REFERENCE: INDETERMINATE STRUCTURAL ANALYSIS, KINNEY, 1957,
* ADISON-WESLEY PUBLISHING CO., PAGE 113, PROBLEM 4-38
*
UNIT FEET KIP
JOINT COORDINATES
1 0 3 0; 2 0 0 0; 3 4 0 0; 4 14 10 0; 5 22 10 0;
MEMBER INCIDENCES
1 1 2; 2 2 3; 3 3 4; 4 4 5;
UNIT INCHES KIP
MEMBER PROPERTY AMERICAN
1 TO 4 PRIS AX 10 IZ 200
DEFINE MATERIAL START
ISOTROPIC MATERIAL1
E 30000
POISSON 0.290909
END DEFINE MATERIAL
CONSTANTS
MATERIAL MATERIAL1 ALL
SUPPORTS
5 FIXED
LOAD 1 HORIZONTAL JOINT LOAD
JOINT LOAD
1 FX 3
PERFORM ANALYSIS
PRINT JOINT DISPLACEMENTS LIST 1
FINISH
