TR.28.2.2 Check Irregularities
STAAD.Pro can check irregularities per the IS 1893 2016 and ASCE 7-05/10/16 seismic codes.
For IS 1893 2016, the program can check horizontal irregularities (torsional and reentrant corners) per Table 5 and vertical irregularities (mass irregularities and irregular modes of oscillation) per Table 6.
For ASCE 7-05/10/16, the program can check horizontal irregularities (torsional and reentrant corners) and vertical irregularies (mass). Irregular modes of oscillation are not considered for this code.
Torsion Check per ASCE 7
Torsion checks per Cl. 12.3.2.1 of ASCE 7 2016 ( ref. fig C12.3-1 Type 1) are preformed by applying unit loads in each orthogonal direction to the control node of the diaphragm.
The unit load, Fx, is applied at each diaphragm in the X-direction. After analysis, the program locates the extreme nodes of the diaphragm and then dmin and dmax are calculated. The ratio of dmax/dmin is evaluated and compared to the code limit of 1.5. This process is then repeated in the Z direction for this diaphragm. Then the similar process is applied to the other diaphragms in the structure.
Torsion Check per IS 1893
Torsion checks per Table 5(i)-a IS 1893 2016 are performed by applying a unit force in each orthogonal direction at two different distances (the design eccentricity, edi) as per Cl. 7.8.2. This results in evaluating four different conditions for IS 1893 2016. The analysis is run and the displacements of the two extreme ends of the diaphragm are extracted from the analysis results. This ratio of these displacements is then reported with a status based on the following limits:
| Ratio | Status | Description |
|---|---|---|
| Δmax/ Δavg < 1.2 | OK | Indicates that the floor is regular and passes the irregularity checks. |
| 1.2 ≤Δmax/ Δavg ≤1.4 | Warning | Indicates that the floor is irregular and requires a full 3D dynamic analysis in order to justify the structural configuration or requires a change in structural configuration as per Cl. 7.1, Table 5, Sl No. (i) sec-i.a and sec-i.b. |
| Δmax/ Δavg > 1.4 | Fails | Indicates that the floor is irregular and fails the irregularity checks. The structural arrangement must be changed as per Cl. 7.1, Table 5, Sl No. (i) sec-ii. |
| (Design eccentricity per IS 1893 2016 Cl. 7.8.2) |
| = | ||
| = |
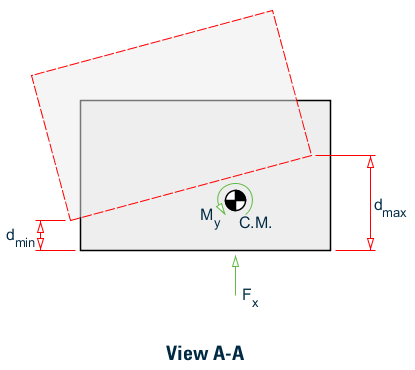
Example floor diaphragm torsion for IS 1893
The unit load, Fx is applied at each diaphragm in the X-direction in combination with two cases of My = Fx× (edi - esi) representing the to cases for edi. After analysis, the program locates the extreme nodes of the diaphragm and then Δmin, Δmax, and Δavg values are calculated. The ratio of Δmax/Δavg is evaluated per the table above. This process is then repeated in the Z direction for this diaphragm for a total of four cases at each diaphragm. Then the similar process is applied to the other diaphragms in the structure.
Reentrant Corners
The program will check for reentrant corners per Table 5(ii) of IS 1893 2016 and Cl. 12.3.2.1 of ASCE 7 2016 ( ref. fig C12.3-1 Type 2). The program first automatically identifies the boundary topology of the diaphragm. That is, the order in which analytical members and nodes of the boundary of the diaphragm are joined together to for a closed polygon. The program then determines the reentrant, or concave, corners of the diaphragm. The two analytical members joining the reentrant node is determined, their lengths are calculated, and then the projections of those lengths are calculated. To determine the ratios, the following are calculated:
Li×cos(α)/Lx ≤ 0.15
Li×cos(α)/Lz ≤ 0.15
If both members from the reentrant node are orthogonal, then for each member, only 1 ratio is calculated as Li/Lx for members oriented along the x-direction and Li/Lz for members oriented along the z-direction.
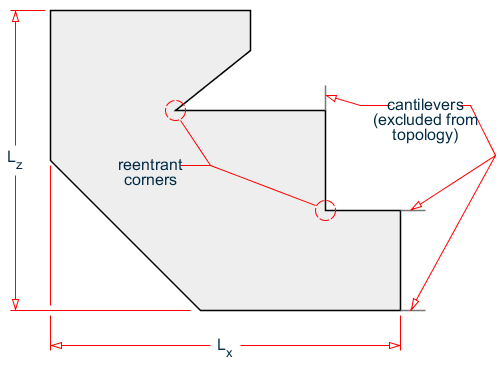
Example reentrant corner topology
All dependent nodes that form part of a diaphragm must lie within the same plane. Further, the boundary dependent nodes must form a closed polygon. Improper modeling of diaphragms may yield incorrect irregularity status results.
Mass Irregularities
The program will check for mass irregularities per Table 6(ii) of IS 1893 2016 and Cl. 12.3.2.2 of ASCE 7 2016 (ref. fig C12.3-2 Type 2). The mass of each floor is calculated as the total of all floor diaphragm masses at the same level. The ratio of each floor mass to the floor above and below is calculated. These ratios are compared to the code stipulated values.
Irregular Modes of Oscillation
Per Table 6(vii)-a, the sum of the percentage of mass participation for the first 3 lateral translational modes should contribute at least 65% in each principle plan direction. This is checked in both orthogonal directions.
Per Table 6(vii)-b, the time period for the fundamental modes in one direction should differ by at least 10%.
IS 1893 2016 Example
An example using IS 1893 2016:
FLOOR DIAPHRAGM DIA 1 TYPE RIG HEI 3 DIA 2 TYPE RIG HEI 6 DIA 3 TYPE RIG HEI 9 CHECK IRREGULARITIES CODE IS1893 2016
ASCE 7 Example
An example using ASCE 7:
FLOOR DIAPHRAGM DIA 1 TYPE RIG HEI 0 DIA 2 TYPE RIG HEI 5 CHECK IRREGULARITIES CODE ASCE7
IS 1893 2016 Example Output
An example output section of an IS 1893 2016 seismic irregularities check:
-IRREGULARITY CHECKS
STAAD.PRO IRREGULARITIES CHECK - ( IS1893-2016 ) v1.2
*********************************************************
Including Amendment no. 2 November 2020
*********************************************************
--TORSION IRREGULARITY CHECKS
Torsion Irregularity Check
Ref: Table 5 (i) - Ratio Limit(s): Lower-1.20 Upper-1.40
---------------------------------------------------------------------
edi : Design Eccentricity
esi : Static Eccentricity
bi : Floor/Diaphragm plan dimension perpendicular to force direction
For Details Refer Clause 7.8 IS1893:2016-Part-1
---------------------------------------------------------------------
Using edi = 1.5esi + 0.05bi
---------------------------
Displacement of extreme points of diaphragm(dia.) in X dir.
------------------------------------------------------------------------
Dia. Node Max. Disp. Node Min. Disp. Avg. Disp. Max./Avg. Status
(mm) (mm) (mm) Disp.
------------------------------------------------------------------------
1 7 0.4984 2 0.4662 0.4823 1.0333 PASS
2 12 2.4871 9 2.3990 2.4430 1.0180 PASS
3 16 6.1637 13 6.0157 6.0897 1.0122 PASS
Using edi = esi - 0.05bi
------------------------
Displacement of extreme points of diaphragm(dia.) in X dir.
------------------------------------------------------------------------
Dia. Node Max. Disp. Node Min. Disp. Avg. Disp. Max./Avg. Status
(mm) (mm) (mm) Disp.
------------------------------------------------------------------------
1 2 0.4984 7 0.4662 0.4823 1.0333 PASS
2 9 2.4871 12 2.3990 2.4430 1.0180 PASS
3 13 6.1637 16 6.0157 6.0897 1.0122 PASS
Using edi = 1.5esi + 0.05bi
---------------------------
Displacement of extreme points of diaphragm(dia.) in Z dir.
------------------------------------------------------------------------
Dia. Node Max. Disp. Node Min. Disp. Avg. Disp. Max./Avg. Status
(mm) (mm) (mm) Disp.
------------------------------------------------------------------------
1 3 0.2699 2 0.2383 0.2541 1.0622 PASS
2 10 1.0087 9 0.9347 0.9717 1.0381 PASS
3 14 2.0463 13 1.9160 1.9812 1.0329 PASS
Using edi = esi - 0.05bi
------------------------
Displacement of extreme points of diaphragm(dia.) in Z dir.
------------------------------------------------------------------------
Dia. Node Max. Disp. Node Min. Disp. Avg. Disp. Max./Avg. Status
(mm) (mm) (mm) Disp.
------------------------------------------------------------------------
1 3 0.3916 2 0.2319 0.3118 1.2562 WARNING*
2 10 1.3253 9 0.9131 1.1192 1.1841 PASS
3 14 2.5782 13 1.8732 2.2257 1.1584 PASS
*** WARNING: The floor is irregular. Please ensure conformance
with Cl. 7.1, Table 5, Sl No. (i) sec-i.a or sec-i.b.
ASCE 7 Example Output
An example output section of an ASCE 7-2016 seismic irregularities check:
STAAD.PRO IRREGULARITIES CHECK - ( ASCE7-2016 ) v1.0
*****************************************************
--TORSION IRREGULARITY CHECKS
Torsion Irregularity Check
Ref: Fig. C12.3-1 T1- Ratio Limit(s): 1.20, 1.40
------------------------------------------------
Dia. Extreme Points of Dia in X Extreme Points of Dia in Z
Node Disp. Node Disp. Node Disp. Node Disp.
(mm) (mm) (mm) (mm)
------------------------------------------------------------------------
1 3 0.09130 1 0.09993 4 0.09484 1 0.10559
2 15 0.29636 13 0.30993 16 0.29819 13 0.34410
Diaphragm ΔX-max/avg ΔZ-max/avg Status
--------------------------------------
1 1.0451 1.0537 OK
2 1.0224 1.0715 OK
--GEOMETRY IRREGULARITY CHECKS
Re-Entrant Corner Check.
(Ref: Fig. C12.3-1 T2- Ratio Limit: 0.15 )
------------------------------------------
Node Re-Entrant X-Proj X-Proj/Lx Z-Proj Z-Proj/Lz Status
Connectivity Node ( m) ( m)
----------------------------------------------------------------------
6-> 5 0.0000 0.0000 7.0000 0.7778 Re-Entrant
4 1.0000 0.2000 0.0000 0.0000
18-> 17 0.0000 0.0000 7.0000 0.7778 Re-Entrant
16 1.0000 0.2000 0.0000 0.0000
Diaphragm: Lx: Lz:
( m) ( m)
----------------------------
1 5.0000 9.0000
2 5.0000 9.0000
--MASS IRREGULARITY CHECKS
Mass Irregularity Check
Ref: Fig. C12.3-2 T2- Ratio Limit: 1.50
---------------------------------------
Dia. Level Mass Above Below Ratio Ratio Status
( m) ( kN) ( kN) ( kN) Above Below
---------------------------------------------------------------------
1 0.000 341.643 253.287 Base 1.349 N/A OK
2 5.000 253.287 Top 341.643 N/A 0.741 OK

